Gradient Descent
Gradient Descent 알고리즘을 enuSpace-Tensorflow를 이용한 사용 방법을 설명합니다.
참고 : https://hunkim.github.io/ml/ (모두를 위한 머신러닝/딥러닝 강의)
Python를 이용한 구현
import tensorflow as tf
x_data = [1., 2., 3.]
y_data = [1., 2., 3.]
W = tf.Variable(tf.random_uniform([1],-10.0, 10.0))
X = tf.placeholder(tf.float32)
Y = tf.placeholder(tf.float32)
hyphothesis = W * X
cost = tf.reduce_mean(tf.square(hyphothesis - Y))
descent = W - tf.mul( 0.1, tf.reduce_mean(tf.mul( (tf.mul(W,X)-Y), X ) ))
init = tf.initialize_all_variables()
sess = tf.Session()
sess.run(init)
for step in range(20):
sess.run(W.assign(descent), feed_dict={X:x_data, Y:y_data})
print( step, sess.run(cost, feed_dict={X:x_data, Y:y_data}), sess.run(W))
enuSpace-Tensorflow를 이용한 구현
Tensorflow의 그래픽 컴포넌트를 이용하여 위와 동일한 코드를 그래픽 컴포넌트를 이용하여 로직을 구성하여 실행한 결과는 아래 그림과 같다. 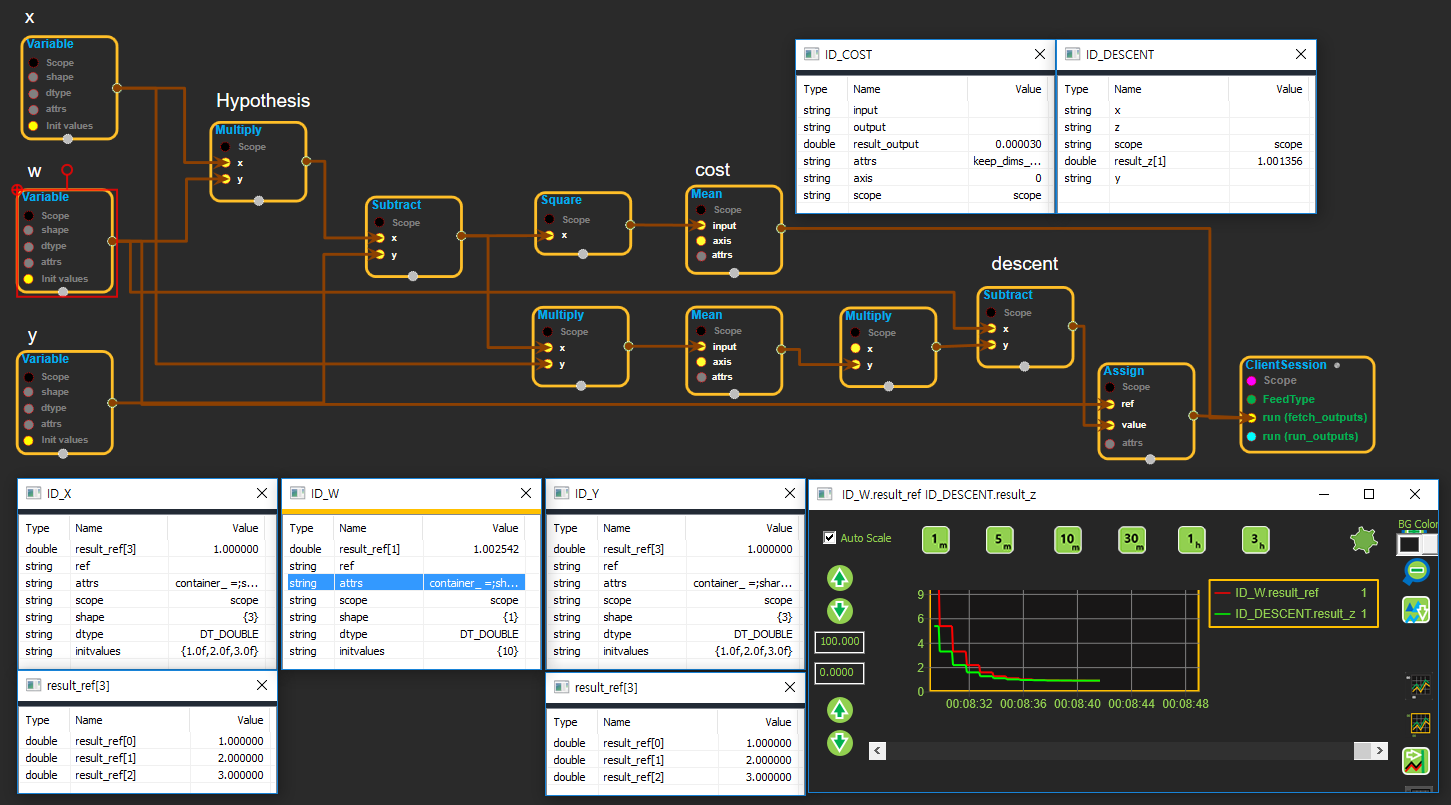 X의 초기값에 {1.0f, 2.0f, 3.0f} 입력시 출력 Y {1.0f, 2.0f, 3.0f}에 해당하는 W값을 구현하는 로직이다.
X의 초기값에 {1.0f, 2.0f, 3.0f} 입력시 출력 Y {1.0f, 2.0f, 3.0f}에 해당하는 W값을 구현하는 로직이다.
자세한 알고리즘에 대한 설명은 https://hunkim.github.io/ml/ (모두를 위한 머신러닝/딥러닝 강의)를 참고하시기 바랍니다.
ApplyGradientDescent 블럭을 이용한 구현 예시
ApplyGradientDescent Equation (var = var - alpha*delta)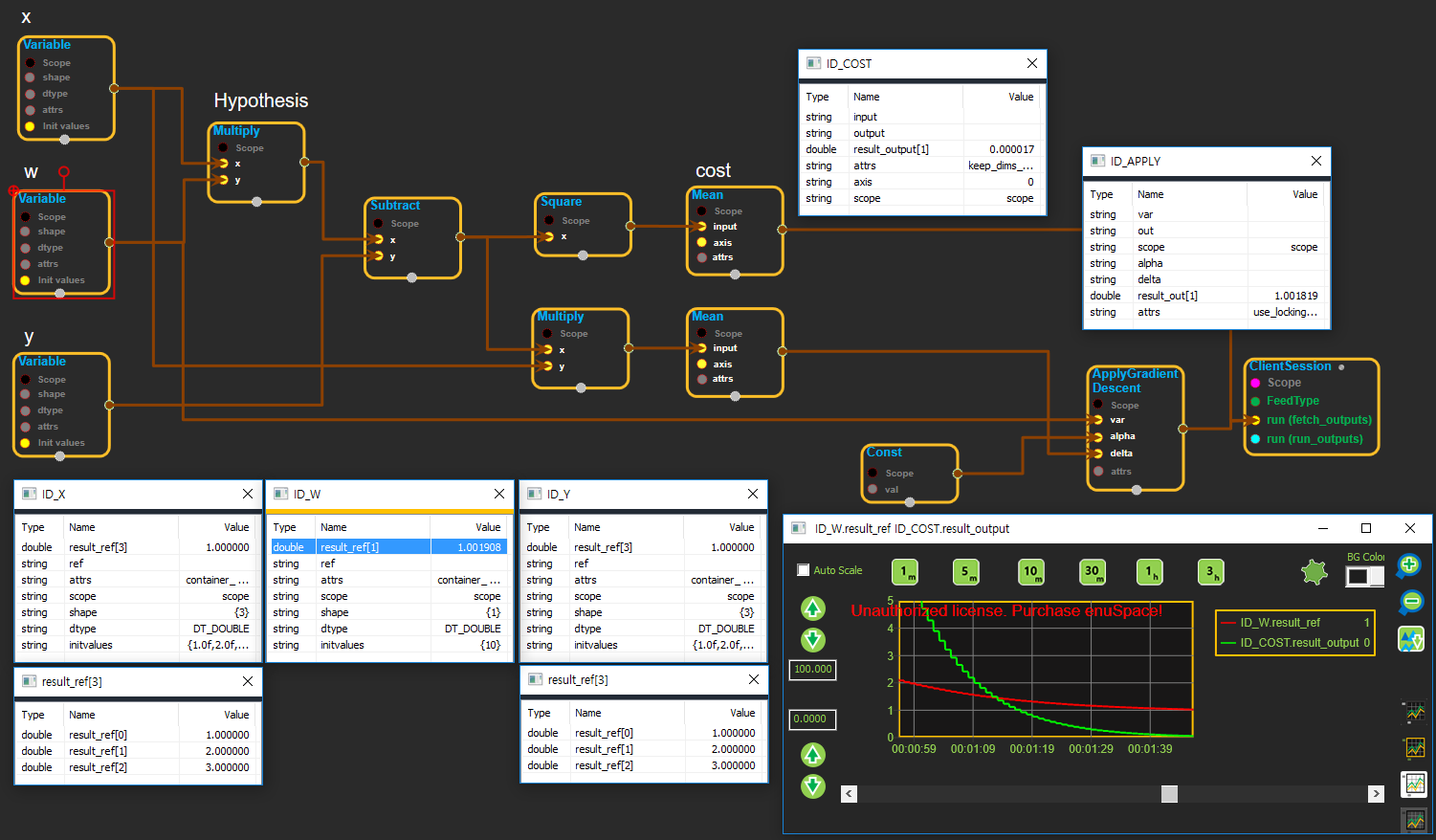
Multi Variable Linear regression 구현 예시
아래의 테이블의 값을 이용하여 W, b의 찾기 위한 그래픽 블럭을 구성하여 예상된 가중치와 바이어스값을 확인.
| X1 | X2 | X3 | Y |
|---|---|---|---|
| 1 | 5 | 21 | 79 |
| 15 | 12 | 22 | 110 |
| 35 | 13 | 23 | 135 |
| 4 | 45 | 24 | 171 |
| 5 | 15 | 53 | 199 |
| 6 | 44 | 7 | 120 |
| 12 | 17 | 27 | 132 |
| 6 | 20 | 28 | 135 |
미리계산된 W, Bias 값 (W1 = 1, W2 = 2, W3= 3, Bias = 5)
Hypothesis Using matrix
H(x1, x2, x3) = x1w1 + x2w2 + x3w3
Multi variable Python 코드 구현예시
x_data = [[1., 5., 21.], [15., 12., 22.],
[35., 13., 23.], [4., 45., 24.], [5., 15., 53.],
[6., 44., 7.], [12., 17., 27.], [6., 20., 28.]]
y_data = [[79.], [110.], [135.], [171.], [199.], [120.], [132.], [135.]]
# placeholders for a tensor that will be always fed.
X = tf.placeholder(tf.float32, shape=[None, 3])
Y = tf.placeholder(tf.float32, shape=[None, 1])
W = tf.Variable(tf.random_normal([3, 1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')
# Hypothesis
hypothesis = tf.matmul(X, W) + b
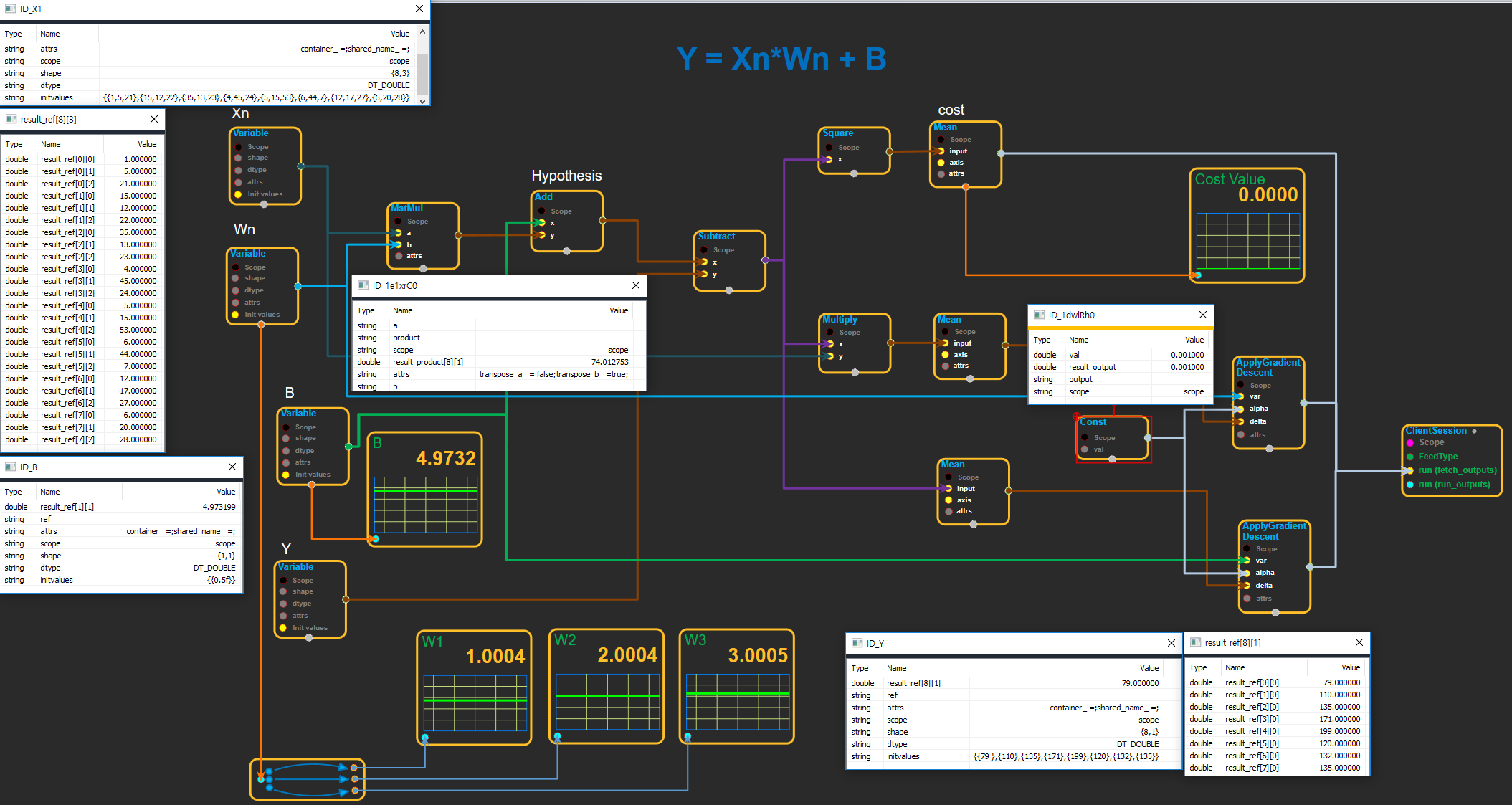
그랙픽 블럭 구성 및 실행 결과
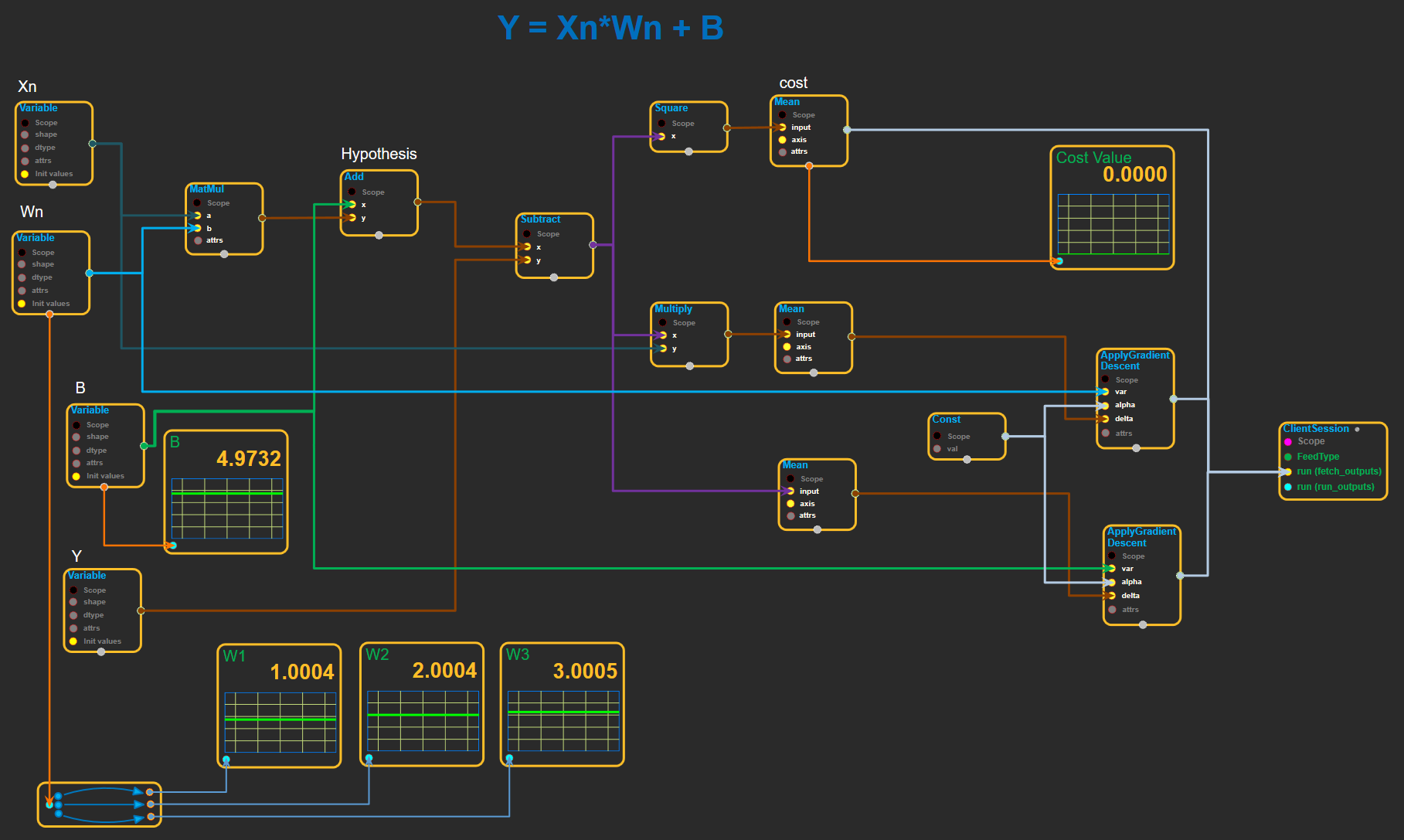 W1, W2, W3의 값이 1, 2, 3의 값으로 수렴, Bias 값 5로 수렴
W1, W2, W3의 값이 1, 2, 3의 값으로 수렴, Bias 값 5로 수렴
초기값 설정
X = {{1,5,21},{15,12,22},{35,13,23},{4,45,24},{5,15,53},{6,44,7},{12,17,27},{6,20,28}}
Y = {{79 },{110},{135},{171},{199},{120},{132},{135}}
W 초기값 = {{1.5,3.5,0.5}}
b 초기값 = {{0.5}}
ApplyGradientDescent alpha 값 = 0.001